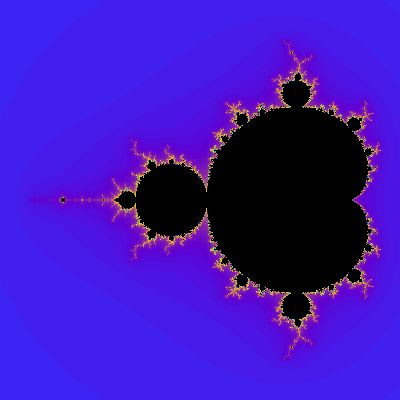
Set of Mandelbrot
As you can see in my CV, my line of research is Fractal Urban Morphology. That´s why I´m so interested in fractals. I´m still reading Pi in the Sky, by John D. Barrow and I´ve already ordered The Artful Universe, same author, it seems promising to me.
Well, in Chapter ¨Footsteps through Plato´s footnotes¨ Barrow says that Pythagoreans began to see things solely as numbers, that are immanent property of things; that is numbers are ¨in¨ things and cannot be separated or distinguished from them in any way. As a contrary point of view, I read that Plato maintained that we discover the truths and theorems of mathematics: we do not simply invent them; for him, mathematics is an (wonderful) example of a particular form of knowledge that owed nothing to the process of human recognition.
Then, in chapter ¨The Platonic world of mathematics¨ (p. 261), Barrow says that the most famous exponent of Platonism was undoubtedly Kurt Gödel. And, what ´s more important for me ¨Most recently, the belief in ¨Pi in the sky¨ Platonism in mathematics has been forcefully restated by Roger Penrose who uses the example of the intricacy of structure displayed by fractals like the Mandelbrot set, which he claims ¨is not an invention of the human mind: it was a discovery. Like Mount Everest,... it is just there¨, to argue that this bottomless structure is not invented by the mind, rather,
though defined in an entirely abstract mathematical way, nevertheless (it has) a reality about it that seems to go beyond any particular mathematician´s conceptions and beyond the technology of any particular computer... it seems clearly to be ¨there¨, somewhere, quite independently of us or our machines.¨ (P.262)
Above, the set of Mandelbrot and three variations. All fractals generated by arq. Myriam Mahiques



No comments:
Post a Comment