The Chaos game. IFS Fern structure generated by Myriam Mahiques. See the difference for both iterations.
Michael Fielding Barnsley is a researcher mathematician who has worked on fractal compression. By the time Mandelbrot had resolved his set, Barnsley was taking a different road. He was thinking about nature’s images and patterns generated by living organisms. He experimented with Julia sets, always trying to achieve greater variables. Until he realized that randomness was the basis for modeling natural shapes. He used the term “chaos game” to refer the global construction of fractals by means of iterated function systems.
Julia sets, that are outcomes of deterministic processes, proved to have a second valid existence as the limit of a random process. Barnsley suggested an analogy for this situation: one could imagine a map of Great Britain drawn in chalk on the floor of a room. A surveyor could find it complicated to measure this awkward shape with fractal coastlines. But, if grains of rice are thrown into the air, allowing them to fall randomly on the floor, these grains inside the map could be counted. As times goes on, the result begins to approach the area of the map. That is the limit of the random process.
Barnsley and his co-workers produced images of nature by writing down a set of simple rules randomly iterated; the question was how to reverse the process: given a particular shape, how to choose a set of rules. The answer, which he called a “collage theorem” was pretty simple. One can begin drawing the shape to be reproduced. Then, using a computer terminal and a mouse as a pointing device, small copies of this shape would be overlaid on the original image, not exactly on top of it, if needed. A highly fractal shape could easily be tiled with copies of itself and at some level of fractal approximation, every shape could be tiled. However, in Barnsley’s technique, the chances serve as a tool, because the results are deterministic and predictable.
To generate a fern leaf with the chaos game, each new point falls randomly, but gradually the fern emerges.
I take this theory as a reflection for urban patterns. To define a shape, Barnsley had two ways, working in superimposed layers or using falling random points. Applying the concept to urban morphologies, if we use a fractal as an analogical model, we need to understand if the fractal generation is consistent with the urban fabric generation. If not, the fractal will be just a simple drawing in 2D with a similar shape. Nothing else. A fishbone structure, is an abstract simplification of the fern pattern. An analogy for the city, would be an axis (an avenue) and lateral oblique streets. But if the city was planned and not generated by random aggregated houses, Barnsley fern is not a good comparison. Or, we can consider the superimposed layers and find out if it works.
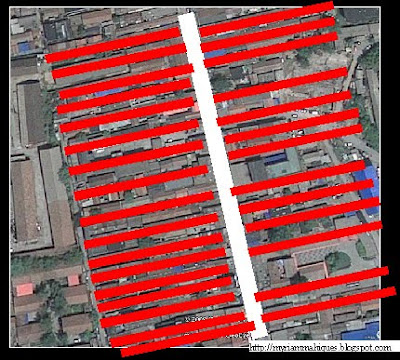
This example of an aerial picture of a neighborhood in China, shows us the different criterion on the subject. Though the regional scale is arranged with cross streets –not exactly a quadrille- the houses are located in straight lines perpendicular to main axes. The first approximation to urban morphology analysis is the Euclidean pattern of lines (houses alignment) across an axis.
Houses alignment. Personal archives.
A fractal pattern discovered through filters. Personal archives.
All patterns together in overlaid layers. Personal archives.
If I decide to work on the image, and see what is behind those lines, I sharpen the edges, make it binary and now I have a fractal pattern with the streets already there, it is not Euclidean any more, as the urban fabric is emphasized over the streets. And if I keep on working, I can see the possibilities of overlapping layers, as Barnsley’s example. That is a more complex fractal image that contains all the information of streets and urban fabric. Compared to Barnsley’s pictures of nature I would say this is a “superfractal”. All three concepts are correct, the difference is which aspect of the urban form will be studied to accomplish our objectives. It is only a matter of professional experience to choose the best one.
REFERENCES
Gleick, James. Chaos. Making a new science. USA. 1987
Barnsley web site:




No comments:
Post a Comment